Question 1

Represent the following game in normal form as a matrix game.

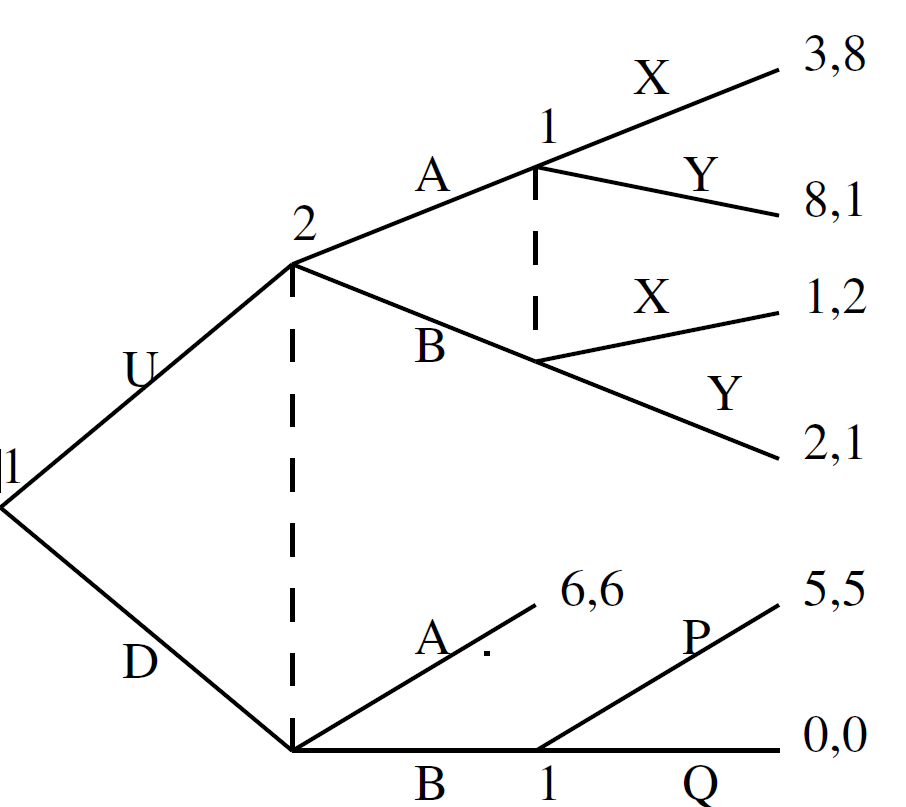
Can you give a different game in extensive form with the same normal form?

Question 2

Suppose that players 1 and 2 have payoff matrices \(A\) and \(B\) respectively where \[A=\left(\begin{array}{rrr} 1 & 0 & -2\\ 3 & 4 & 1\\ 2 & -2 & -2\end{array}\right) \quad\quad B=\left(\begin{array}{rrr} 3 & -1 & 4\\ -2 & 1 & 0\\ -4 & 2 & 1\end{array}\right).\] If player \(A\) chooses each strategy with equal probability and player \(B\) chooses strategy one 10% of the time, strategy two 25% of the time, and strategy three otherwise, calculate the expected values of the game for player 1 and player 2.

Question 3

Use iterated dominance of pure strategies to simplify the following game:

Strategy 1 Strategy 2 Strategy 3 Strategy 4
Strategy 1 \((8,7)\) \((4,2)\) \((5,5)\) \((6,1)\)
Strategy 2 \((2,1)\) \((6,3)\) \((8,0)\) \((1,3)\)
Strategy 3 \((2,3)\) \((5,7)\) \((1,1)\) \((10,6)\)
Strategy 4 \((3,4)\) \((4,5)\) \((8,1)\) \((9,4)\)

Question 4

Consider the game

A B C D
x \((3,6)\) \((4,10)\) \((5,0)\) \((0,8)\)
y \((2,6)\) \((3,3)\) \((4,10)\) \((1,1)\)
z \((1,5)\) \((2,9)\) \((3,0)\) \((4,6)\)

Is there a mixed strategy for player 1 using just two of \(x\), \(y\), \(z\) that dominates the remaining pure strategy?