PhD Index       Documentation Index      

One of the overall aims of this study has been is to develop a set of tools that describe the general geomorphometry of a surface. On the whole, this is quite distinct from the process of identifying specific geomorphometric features such as cirques or floodplains. There are however, a number of surface features that may be used both in the specific and general geomorphometric identification process. These features can be thought of as morphometric features rather than geomorphometric in that they are characteristic of any surface.

The most widely used set of morphometric characteristics, is the subdivision of all points on a surface into one of pits, peaks, channels, ridges, passes and planes (see Figure 5.1). The names of these features suggest a geomorphological interpretation, but they may be unambiguously described in terms of rates of change of three orthogonal components (see Table 5.1). Note that the components x and y are not necessarily parallel to the axes of the DEM, but are in the direction of maximum and minimum profile convexity.

Figure 5.1 - The six categories of morphometric feature illustrated by the relationship between a central DEM cell and its eight neighbours.

Feature name	Derivative expression	Description
Peak		Point that lies on a local convexity in all directions (all neighbours lower).
Ridge		Point that lies on a local convexity that is orthogonal to a line with no convexity/concavity.
Pass		Point that lies on a local convexity that is orthogonal to a local concavity.
Plane		Points that do not lie on any surface concavity or convexity.
Channel		Point that lies in a local concavity that is orthogonal to a line with no concavity/convexity.
Pit		Point that lies in a local concavity in all directions (all neighbours higher).

Table 5.1 - Morphometric Features described by second derivatives.

The identification of these features forms the basis of the techniques described in this chapter for describing DEM characteristics. The first two sections describe how the features themselves may be identified. The third section extends the technique to extract multi-scale behaviour. The final section concentrates on the hydrological implications of the layout of these morphometric features. It is worth noting at this stage that this classification produces point-based categories (pits, passes, and peaks), two line-based categories (channels and ridges) and one area-based category (planes).

5.1 Feature Identification

The standard method of identifying morphometric features is to pass a local (usually 3 by 3) window over the DEM and examine the relationships between a central cell and its neighbours (eg. Peucker and Douglas, 1975; Evans, 1979). Alternative methods exist for terrain modelled with contour lines (eg. Maxwell, 1870; Tang, 1992), but will not be considered here. This section will consider how the multi-scaled parameterisation discussed in the previous chapter may be applied to morphometric feature identification.

5.1.1 Quadratic Approximation

For consistency with the general geomorphometric parameters identified previously, the second derivatives required to identify all six features are extracted using quadratic approximation of some local window (see section 4.4). Cross-sectional curvature (crosc) is used to characterise the second derivative as this is the convexity measure that is most closely related to geomorphological process. At locations with a non-zero slope, channels have a negative crosc, ridges a positive crosc, and (sloping) planes a crosc of zero. Additionally, we can measure the longitudinal curvature longc in order to define the three remaining feature types. Pits have a negative crosc and longc, peaks a positive crosc and longc, and passes crosc and longc with opposite signs.

For cases of zero slope, the slope direction (aspect), crosc and longc remain undefined. In such cases an alternative measure of convexity is required that is not based on slope direction. Young (1978) shows how the maximum and minimum convexity values can be derived from the quadratic coefficients a, b and c for this special case:

For a surface modelled by the quadratic,

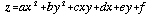. . . . . . . . . . . (5.1)

where gradient is zero (d² = e² = 0), maximum and minimum convexity values are,

. . . . . . . . . . . (5.2)

Together, slope, crosc, longc, minic, and maxic provide a complete and unique set of conditions for defining all six morphometric features (Table 5.2)

Feature	slope	crosc	longc	maxic	minic
Peak	0	#	#	+ve	+ve
	+ve	+ve	+ve	#	#
Ridge	0	#	#	+ve	0
	+ve	+ve	0	#	#
	+ve	0	+ve	#	#
Pass	0	#	#	+ve	-ve
	+ve	+ve	-ve	#	#
	+ve	-ve	+ve	#	#
Plane	0	#	#	0	0
	+ve	0	0	#	#
Channel	0	#	#	0	-ve
	+ve	-ve	0	#	#
	+ve	0	-ve	#	#
Pit	0	#	#	-ve	-ve
	+ve	-ve	-ve	#	#

Table 5.2 Morphometric features defined by the sign of five morphometric parameters. # indicates undefined, or not part of selection criteria.

It becomes necessary to check longitudinal curvature when identifying ridges and channels where the ridge/channel sides are of significantly different heights. In such cases the slopedirection is unlikely to be 'down-channel' (or along the ridge), but obliquely across the length of the feature. Additionally there is a possibility of misclassification for features similar to those illustrated in Figure 5.2. In Figure 5.2(a) the negative cross-sectional curvature (orthogonal to the slope vector represented by an arrow) suggests a channel, but the longitudinal curvature is also negative, forcing classification as a pit. Figure 5.2(b) shows a similar situation where a positive longitudinal curvature forces an apparent channel to be classified as a pass. The result of applying this classification algorithm to a real geomorphological surface is to overrepresent the numbers of point-based categories (peaks, passes and pits).

Figure 5.2 - Two misclassified features due to asymmetric neighbourhoods.

A simplified and improved algorithm for classification is suggested here that preserves the continuity of line-based channels and ridges to a far greater extent. This provides an advantage over traditional methods of feature selection based on logical comparison of neighbours (eg, Peucker and Douglas, 1975; Jensen, 1985; Bennet, 1989; Skidmore, 1990).

It is assumed that all locations that have a local slope must be either planar, form part of achannel or form part of a ridge. Pits peaks and passes are assumed only to occur where local slope is zero. These assumptions are perhaps closer to our own models of the surface features. The anomalous classifications shown in Figure 5.2 are eliminated. The selection criteria are shown in Table 5.3.

Feature	slope	crosc	maxic	minic
Peak	0	#	+ve	+ve
Ridge	0	#	+ve	0
	+ve	+ve	#	#
Pass	0	#	+ve	-ve
Plane	0	#	0	0
	+ve	0	#	#
Channel	0	#	0	-ve
	+ve	-ve	#	#
Pit	0	#	-ve	-ve

Table 5.3 Simplified feature classification criteria.

These rules provide the basis for the morphometric classification considered in the rest of this chapter.

5.2 Slope and Curvature Tolerance

The method described above, if strictly applied will tend to produce surfaces that consist almost entirely of interdigitating channels and ridges. This is because (i) a quantised DEM will rarely produce truly planar facets with profile convexity components of zero (the only relatively common exception being flat regions such as lakes and coastal areas), and (ii) true peaks, passes and pits usually have an overall slope value when their neighbours are considered. Figure 5.3 shows how small variations in one or two values can change the nature of the feature detected. To overcome this two tolerance values are introduced that account for (i) and (ii) above.

Let Tconvex be the minimum crosc that represents a true cross-sectional convexity/concavity. In effect, this value defines the minimum concavity of a channel cross-section and convexity of drainage divides. Let Tslope be the minimum slope that represents a true slope. In effect, this value defines the minimum longitudinal channel or ridge slope in which local variations can occur, without breaking it up with a series of pits, passes and peaks. The values of these tolerances are somewhat arbitrary, yet it is necessary to have the flexibility to vary the feature selection process according to the nature of terrain. The algorithm representing these modified rules is shown in Algorithm 5.1 (coded as part of r.param.scale and d.param.scale in the Appendix). The results of varying the both tolerance values for a mountainous DEM are shown in Figure 5.4 as small multiples (Tufte, 1990). The position of each image within the figure indicates the magnitude of the two tolerance values.

Figure 5.3

Figure 5.4 - Effect of tolerance values on feature classification. Columns represent a relaxing of the slope tolerance (degrees); rows represent increasing curvature tolerance (dimensionless). Features are classified as pits (black), channels (blue), passes (green), ridges (yellow), and peaks (red).

Name: Mfeature(coeff,n) Purpose: Identifies the morphometric feature described by a bivariate quadratic function. Parameters: coeff[6] Array holding the 6 quadratic coefficients a to f n Size of side of local window Globals: Tslope Minimum gradient that defines a non flat surface Tconvex Minimum convexity defining a non-planar surface g Grid resolution of DEM Locals: slope Maximum gradient crosc Cross-sectional convexity minic,maxic Minimum and maximum convexity Mfeature(coeff) { /* Measure morphometric parameters */ slope = atan(sqrt(d*d + e*e)) crosc = n*g*(b*d*d + a*e*e - c*d*e)/(d*d + e*e) maxic = n*g*(-a-b+sqrt((a-b)*(a-b) + c*c)) minic = n*g*(-a-b-sqrt((a-b)*(a-b) + c*c)) /* Identify morphometric features */ if (slope > Tslope) /* Case 1: Surface is sloping */ { if (crosc > Tconvex) return (RIDGE) if (crosc < -Tconvex) return (CHANNEL) else return (PLANAR) } if (maxic > Tconvex) /* Case 2: Surface is horizontal */ { if (minic > Tconvex) return (PEAK) if (minic < -Tconvex) return (PASS) else return (RIDGE) } if (minic < -Tconvex) { if (maxic < -Tconvex) return (PIT) else return (CHANNEL) } return(PLANAR) }

Algorithm 5.1 - Feature classification.

5.3 Multi-scale feature classification

The argument presented in the previous chapter was that one resolution dependent parameterisation is not sufficient to describe surface form. Surface parameters should be able to be expressed at a variety of sizes. Likewise, a rule-based classification of morphometric features based on those parameters should also be multi-scale. If we are to match morphometic 'peaks' to our own geomorphometric understanding, it is very unlikely that the scale defined by the DEM resolution will be sufficient. Thus the rules for feature classification defined above are scale independent. The parameters a-f in (1) can be found for any window size before being used for classification.

The result of applying a multi-scale approach is that each location has multiple feature attributes. These can be visualised in a number of ways. Animation may be used with 'time' representing change in spatial scale (an approach adopted by Wood et al, 1996 for characterising population density surfaces). Alternatively, small multiples may be used to show the 'slices' through this sequence (see Chapter 6 for examples of this). The third alternative that is adopted here for an interactive visualisation context, is the multi-scale 'probe'. A mouse is passed over a DEM so that when a mouse button is clicked, the feature classification of the relevant DEM cell is found over a range of window sizes. The result is a graphical representation of the feature membership function. Equally important is an equivalent representation of the morphometric parameters (crosc and slope) used for the classification. The C code for interactive probing in this way is shown in the Appendix (d.param.scale).

Figures 5.5 and 5.6 show an example of this probe applied to part of the Lake District DEM. The cross in the upper image of both figures indicates the point selected for query. In both cases this corresponds to Mickledore - a well known gap between England's two highest mountains, Scafell Pike (to the North East) and Scafell (to the South West). This location would probably be considered by most visitors to the location as a 'pass' with two steep gullies running orthogonally to the direction of the two peaks on either side. Yet if we are to classifythe point location, the type of feature should (and does) depend on the scale of interest. The lower image in both figures shows the relationship between the parameter or feature classification and local window size. The X-axis in both figures ranges from 3 x 3 cells at the origin to 69 x 69 cells at the right hand side. At the resolution of the DEM this corresponds to a spatial range of 150m to 3.5km. The extent of the kernel shown graphically in Figure 5.7 with kernels 3x3 to 29x29 shown as red squares, and kernel boundaries indicated for sizes 39x39, 49x49, 59x59 and 69x69.

Figure 5.5

Figure 5.6

Figure 5.7

Both cross-sectional curvature and feature type vary with scale. Short lags would indicate that the location is part of a convex channel. As the scale is widened, it is revealed that this channel lies within a larger pass, that itself is part of an extended convex ridge. The largest lags indicate a peak feature. It is suggested that this scale based progression of characteristics is much more useful than a single morphometric parameter or classification. It provides a landform signature (Pike, 1988) that is more discriminating that a single feature classification, but sufficiently general to be of use in an analytical context.

There are likely to be contexts when a single measure or classification is required, so it is useful to at least quantify the variability of measurements. For (the ratio scale) parameters, the mean and standard deviation are calculated. For the categorical feature classification, the mode and scaled entropy is calculated,

. . . . . . . . . . . (5.3)
where p(f_i) is the proportion of measurements classified as feature type i and n is the number of feature types (6 in this study).

This may be used to distinguish locations that are consistently classified as the same feature (E_s = 0) from locations that have a high degree of scale dependency in their classification (E_s = 1). While this form of interrogation is useful in an interactive visualisation context, it is difficult to identify the spatial pattern of entropy across the image. To visualise both the spatial distribution and scale dependency of measures it is necessary to create several raster layers containing morphometric feature classification at a range of scales. Using simple map algebra, these maps can be combined to produce two new images, one of the modal classification, the other of entropy (see Algorithm 5.2). Thus it is possible to produce a feature membership map and a classification uncertainty map. These may be combined into a single hue-intensity image (see Chapter 6).

# Map Algebra script for calculating modal classification of morphometric # features. Creates two maps, one of modal classification, one of entropy. # # Note: feat9, feat15, feat21 etc. are the map layers containing feature # classification at the corresponding kernel sizes. # pplne,ppit,pchan etc. contain the proportion of maps classified # in each feature category. r.mapcalc << EOF pplne = (feat9 ==0) + (feat15==0) + (feat21 == 0) + (feat27 == 0) + (feat33 == 0) + (feat45 == 0) ppit = (feat9 ==1) + (feat15==1) + (feat21 == 1) + (feat27 == 1) + (feat33 == 1) + (feat45 == 1) pchan = (feat9 ==2) + (feat15==2) + (feat21 == 2) + (feat27 == 2) + (feat33 == 2) + (feat45 == 2) ppass = (feat9 ==3) + (feat15==3) + (feat21 == 3) + (feat27 == 3) + (feat33 == 3) + (feat45 == 3) pridg = (feat9 ==4) + (feat15==4) + (feat21 == 4) + (feat27 == 4) + (feat33 == 4) + (feat45 == 4) ppeak = (feat9 ==5) + (feat15==5) + (feat21 == 5) + (feat27 == 5) + (feat33 == 5) + (feat45 == 5) entrop = 1000* ((pplne/6.0)*log(.001 + pplne/6.0) + (ppit/6.0)*log(.001 + ppit/6.0) + (pchan/6.0)*log(.001 + pchan/6.0) + (ppass/6.0)*log(.001 + ppass/6.0) + (pridg/6.0)*log(.001 + pridg/6.0) + (ppeak/6.0)*log(.001 + ppeak/6.0)) / log(1.0/6.0) mode = (max(pplne,ppit,pchan,ppass,pridg,ppeak)==pplne)*0 + (max(pplne,ppit,pchan,ppass,pridg,ppeak)==ppit)*1 + (max(pplne,ppit,pchan,ppass,pridg,ppeak)==pchan)*2 + (max(pplne,ppit,pchan,ppass,pridg,ppeak)==ppass)*3 + (max(pplne,ppit,pchan,ppass,pridg,ppeak)==pridg)*4 + (max(pplne,ppit,pchan,ppass,pridg,ppeak)==ppeak)*5 EOF

Algorithm 5.2 - Classification membership calculation using map algebra.

5.4 Hydrological Modelling

One of the most direct relationships between geomorphological form and process is that between fluvial and hydrological process and resultant features. This is one of the most widely examined relationships that may be derived from a DEM (see section 2.3). There are several reasons for this pertinent to the objectives of this study. Firstly, although fluvial process results in geomorphological form, the process may be inferred from the nature of that form at the scale of the DEM. This is a relatively rare two way relationship (compare, for example, with other process such as frost heave, longshore drift, weathering etc.). It suggests that the use of GIS-based analysis of DEMs can progress beyond the characterisation of form to an assessment of surface process. Consequently fluvial and hydrological modelling have many immediate applications in the GIS arena. Secondly, fluvially eroded channels are comparatively unambiguously defined geomorphological features that can be represented using a DEM. There is of course, a scale dependency in the effectiveness of this channel modelling. Thirdly, and most importantly in the context of this study, hydrological processes allow us to define important spatial properties of a surface. The drainage basin represents a fundamental geomorphological areal unit, providing both an hierarchical and exhaustive spatial sub-division. Its clear scale dependency is appropriate to the style of analysis adopted in this study, and so will be considered in a little more detail here.

This section will not consider the extraction of drainage networks explicitly. This has been investigated by many authors elsewhere (see section 2.3). It has already been suggested that many of the problems associated with drainage network identification are due to a failure to consider an appropriate range of scales in classification. Some of these problems could be overcome by adopting the multi-scale feature classification described in the previous section. The connected macro-scale valley networks identified with larger kernels can be used to force hydrological connectivity at the raster cell scale. For more details of this style of approach (albeit in a rather more primitive form) see Wood (1990b).

5.4.1 Drainage basin identification

The identification of the drainage basin is an important process in both characterising a surface and in defining spatial units that are appropriately related to geomorphological process. The method for basin identification adopted here also identifies two allied and important surface characteristics. Firstly, basin delineation implies the identification of drainage divides - a linear network whose topology and geometry provide useful summaries of a surface's form. Secondly, a modelled flow magnitude surface is produced. Each location on this surface has a value associated with the proportion of surface flow that might be expected to pass over it. This has long been used to identify drainage networks (eg Mark, 1983a). The topology of this surface could be characterised in much the same way as blue-line drainage networks (Shreve, 1966).

Most basin identification algorithms involve a 'basin climbing' approach where a basin outflow point is identified and the basin is recursively 'climbed' until all points flowing from the drainage divide have been covered (eg. Marks et al, 1983). This is broadly the approach adopted here (see r.basin in the Appendix) . There are, however, a number of problems associated with identifying drainage basins in this way. If a single outflow cell is missed at the base of a steep sided valley, diagonal or orthogonal basin edges can be produced running up the sides of the valley walls. If hydrological consistency is required, pits in the surface halt recursive algorithms that only travel 'upstream' from an outlet (eg Band, 1989). The result is either a basin identification routine that does not work, or the production of internal basins with no apparent outflow. Yet the occurrence of measured pits is relatively common in mountainous terrain where the valley neck is narrow (eg cirque formation). The valley neck itself may not be picked up at the (planimetric) scale of the DEM, or the terrain at the neck may be sufficiently flat to allow elevation uncertainty to dominate.

A number of possible solutions may be applied to this 'problem'. Pits can be filtered out as a preprocessing option. This may however, (arbitrarily) change elevation values unnecessarily. Alternatively, internal basins may be merged as a post-processing operation. This may be achieved by either 'excavating' cells that connect the base of a pit to its adjacent downstreambasin, or by flooding pits until outflow is redirected. The latter is adopted here (see r.basin in the Appendix). Figure 5.8 shows the effect of recursive pit removal on basin derivation for a 30x30km region of the Lake District. Superimposed on (a) and (b) is the distribution of flooded pits (in shades of red). In all cases, internal basins (a) contain at least one of these pits. The basins in Figure 5.8(b) correspond to the major valley systems of this part of the Lake District (clockwise from the top, cyan, Borrowdale; mauve, Thirlmere valley; pink, Ullswater valley; blue, Windermere/Coniston valleys; purple, Dunnerdale; plum Eskdale; pink, Wasdale).

Figure 5.8

For geomorphological characterisation (as opposed to hydrological analysis) it is arguable whether the identification of internal drainage basins is in fact a problem. Valley systems with narrow necks should be represented as pits at some scale. It is only a problem for hydrological modelling that the mechanism for water removal is expressed at a different scale. The relationship between basin delineation (not hydrologically enforced) and scale is shown in Figure 5.9. Quadratic approximation is used to smooth the DEM with kernel sizes up to 950m. The basin finding routine was then applied to the smoothed surfaces. As expected the number of basins decreases with generalisation, although not spatially consistent.

Figure 5.9