Introduction of Computer Codes produced from research of Prof. Ma and his group

QALE_FEM/FLOATMov

This code can model 3D extremely steep waves and overturning waves, as well as their interaction with single and multiple floating bodies. According to our numerical tests, this code can be at least 10 time fasters than others with similar capacity.

Most relevant publications including:

· Ma, Q.W. and Yan, S., 2006, “Quasi ALE finite element method for nonlinear water waves”, Journal of Computational Physics, Vol. 212, Issue 1, pp. 52-72.

· Yan, S. and Ma, Q.W., 2006, “Numerical simulation of fully nonlinear interaction between steep waves and 2D floating bodies using QALE-FEM method”, Journal of Computational Physics,Vol. 221, Issue 2, pp. 666-692;

· Ma, Q.W. and Yan, S 2009, “QALE-FEM for Numerical Modelling of Nonlinear Interaction between 3D Moored Floating Bodies and Steep Waves,” International Journal for Numerical Methods in Engineering, Vol. 78, pp. 713-756.

· Yan, S, and Ma, Q.W., 2010, “QALE-FEM for modelling 3D overturning waves,” International Journal for Numerical Methods in Fluids, Vol. 63, pp.743 – 768.

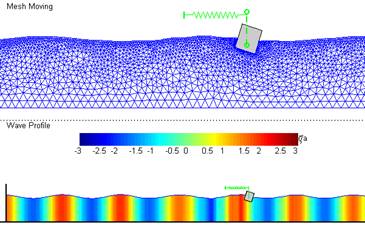
Free response of 2D body in water waves

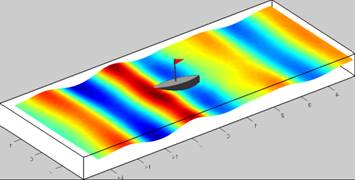
Response of a 3D Wigley Hull to steep waves with a incident angle of 15^o

(please click here to download the movies of the free-response case or here for fixed cases)

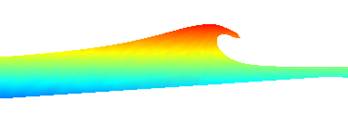
2D Overturning waves (slope of bed: 1:15) (Please click here to download the movie)

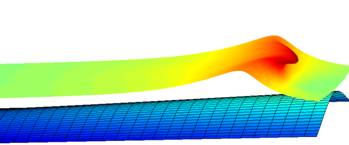
3D Overturning waves on 3D bed

Tank length: 19d; Width: 8d; Initial wave height: 0.6d; slope of bed 1:15; total CPU time: 54 minutes on a normal PC (Pentium Ⅳ 2.53GHz processor, 1G RAM) for the computing period from to

(Please click here to download the movie)

SLOSHWav

This code was developed when Dr Ma worked in University Colleague London (most relevant publications: Wu, G.X., Ma, Q.W and Eatock Taylor R. 1998, "Numerical simulation of sloshing waves based on finite element method", Applied Ocean Research, Vol. 20, pp. 337-355) and can be used to simulate three dimensional sloshing waves in a fluid container subjected to any motion and may be applied to solving a range of engineering problems, such as water flow on deck of ships and offshore floating structures, sloshing motion of oil in oil tanks and water waves in a lake caused by strong winds (if pressure distribution is given) and earthquakes (if the motion caused by earthquake is specified).

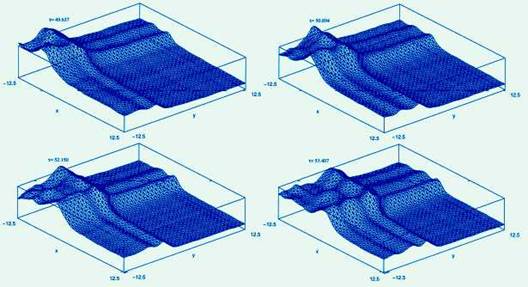
An example of sloshing wave simulated using SLOSHWav is shown in the following figure.Sloshing waves in a square tanks

GENWav

This code was developed when Dr Ma worked in University Colleague London (most relevant publications: Ma, Q.W., Wu, G.X. & Eatock Taylor, R., 2001, "Finite element simulation of fully nonlinear interaction between vertical cylinders and steep waves--part 1 methodology and numerical procedure", Int. J. Numer. Meth. Fluids, Vol. 36, pp. 265-285 and Ma, Q.W., Wu, G.X. & Eatock Taylor, R., 2001, "Finite element simulation of fully nonlinear interaction between vertical cylinders and steep waves--part 2 numerical results and validation", Int. J. Numer. Meth. Fluids, Vol. 36, pp. 287-308) and can be used to numerically simulate the water waves generated by a wavemaker which is subjected to any oscillation that may be monochromatic, bichromatic or random. Some examples simulated using GENWav are shown in the following figure

STRUCWav

This code was developed when Dr Ma worked in University Colleague London (most relevant publications: Ma, Q.W., Wu, G.X. & Eatock Taylor, R., 2001, "Finite element simulation of fully nonlinear interaction between vertical cylinders and steep waves--part 1 methodology and numerical procedure", Int. J. Numer. Meth. Fluids, Vol. 36, pp. 265-285 and Ma, Q.W., Wu, G.X. & Eatock Taylor, R., 2001, "Finite element simulation of fully nonlinear interaction between vertical cylinders and steep waves--part 2 numerical results and validation", Int. J. Numer. Meth. Fluids, Vol. 36, pp. 287-308) and can be used for modeling interaction between water waves and offshore structures with cylindrical legs, such as semi-submerged platforms. The waves are generated by a wave maker at one end of a long tank with a damping zone and Sommerfeld condition implemented at the other end to reduce the wave reflection. Two or four legs structures can be put into the tank. The following figures show some results obtained using this code.

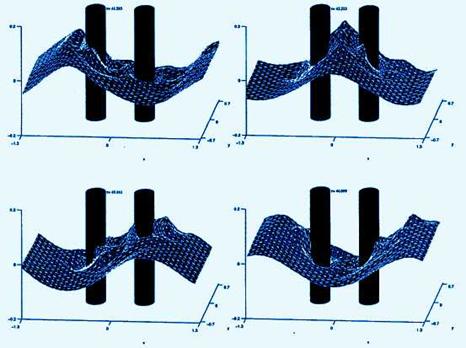
Interaction between steep waves and two cylinders

FLOATMov

This code was developed when Dr Ma worked in University Colleague London and Robert Gordon University (most relevant publications: Ma, Q.W. & Patel, M.H., 2001, “On the nonlinear forces acting on a floating spar platform in ocean waves”, Applied Ocean Research, Vol. 23/1, pp 29-40. and Ma, Q.W. & Patel, M.H.,2002, "Coupled nonlinear motion of floating structures with water columns in open-bottom tanks ", Proceedings of 21st International conference on Offshore Mechanics And Arctic Engineering (Omae'02), June 23–28, 2002 — Oslo, Norway) and can be used to calculate the response of a floating structure with six degrees of freedom in ocean waves. Open bottom tanks may be included in the structure. The amplitude of the motion can be very large because all nonlinear terms in motion equations are taken into account. Some numerical results from this code are shown in the following figure.

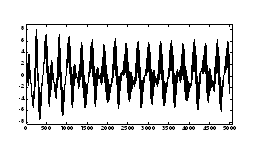
Surge motion of a SPAR platform with open bottom tank

For further details of these codes, please contact Dr. Qingwei Ma via q.ma@city.ac.uk